√99以上 三角形 三平方の定理 115400-三角形 三平方の定理 証明
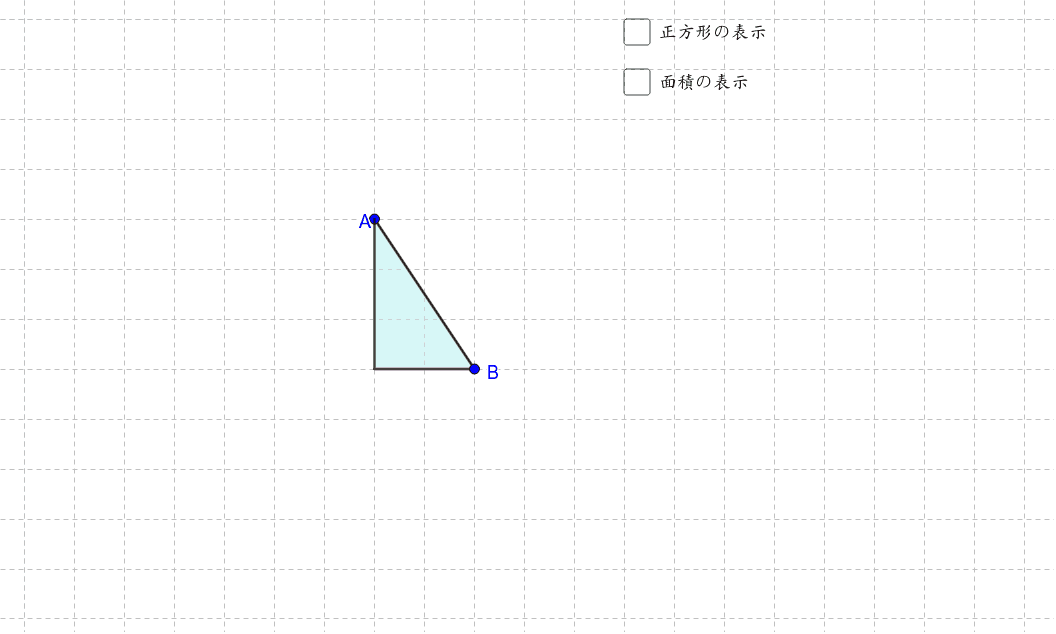
三平方の定理の導入 Geogebra
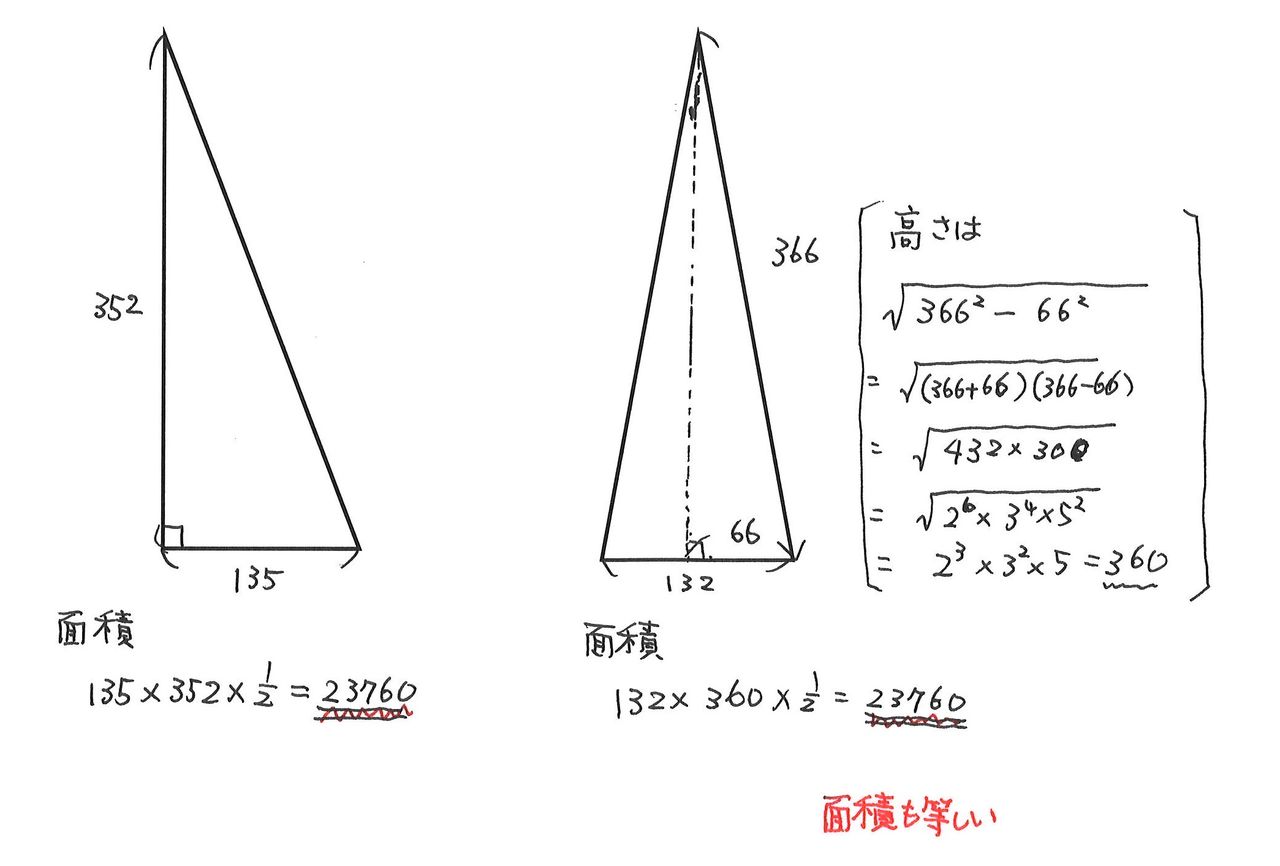
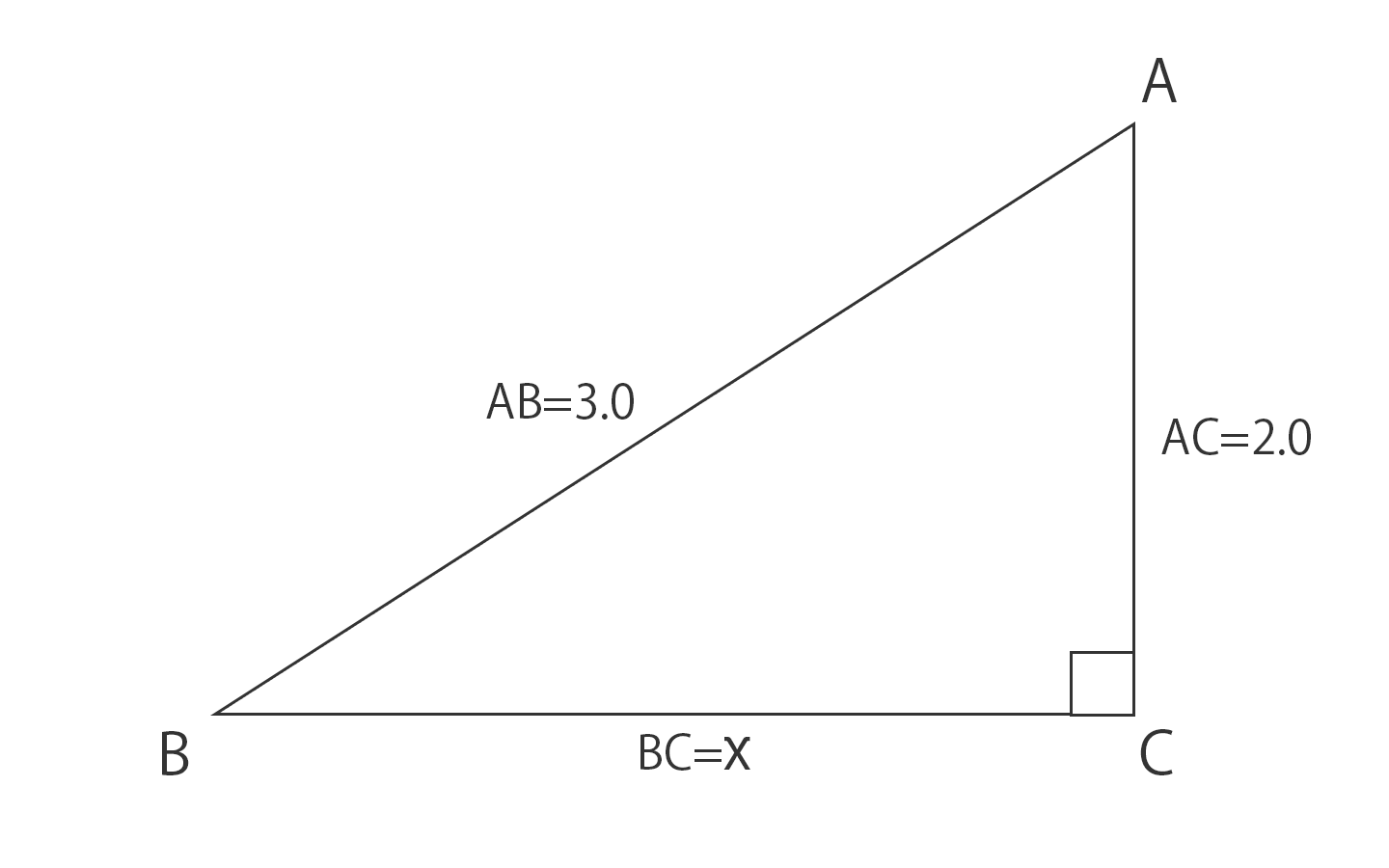
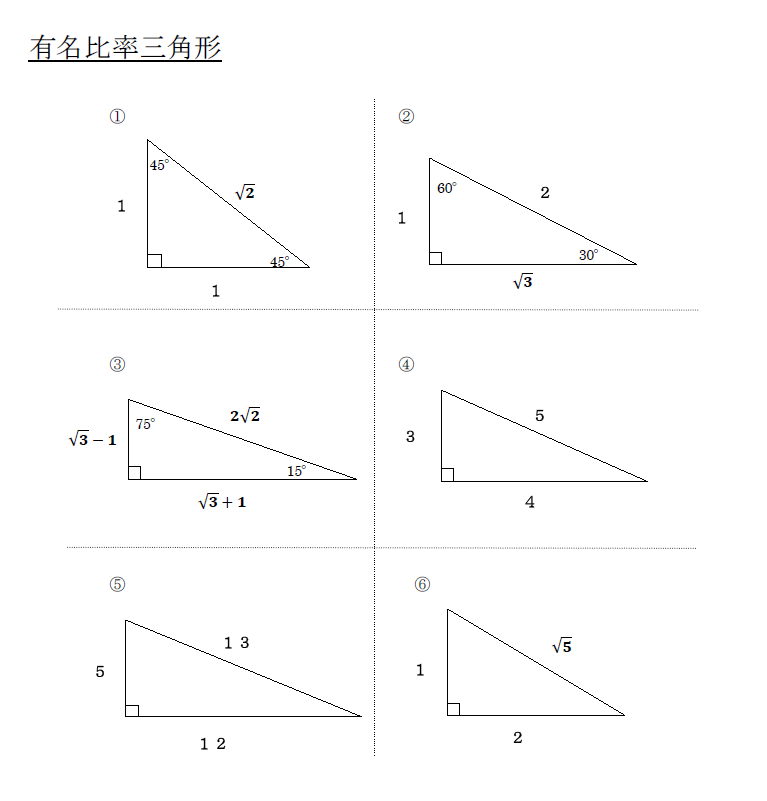
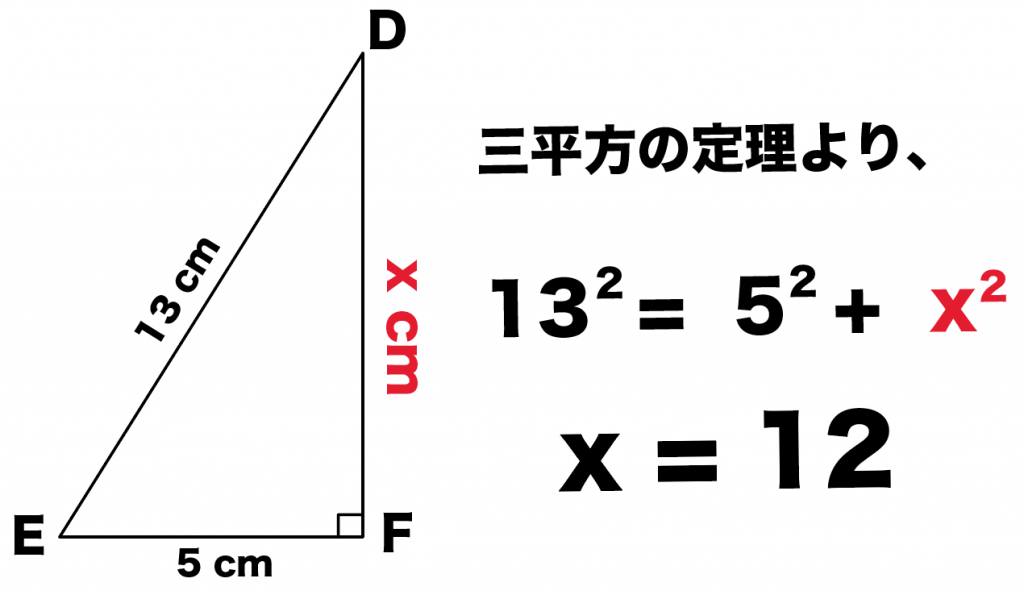
三平方の定理(基本問題1) 例題 次の直角三角形で、xの値を求める。 x 2 6 xが斜辺なので 2 2 6 2 = x 2 x 2 = 40 x = ±2 √ 10 x > 0より x =2 √ 10 x 4 5 斜辺が5なので x 2 4 2 =5 2 x 2 = 2516 x 2 =9 x=±3 x>0より x=3 次の直角三角形で、xの値をそれぞれ求めよ。三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵 が成り立つことを、 三平方の定理 と言います。 三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが 3 c m と 4 c m の直角三角形
三角形 三平方の定理 証明
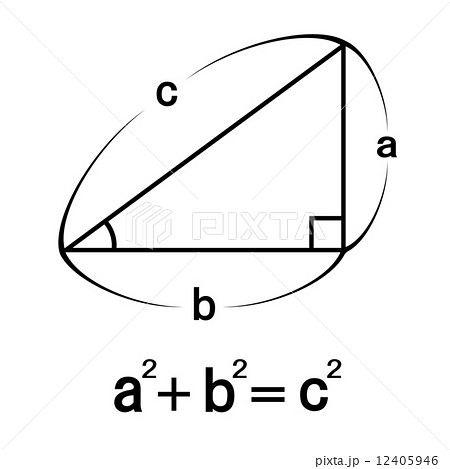
三角形 三平方の定理 証明-三平方の定理の逆 三平方の定理の逆とは、三角形の3辺がa² b² = c² を満たせば、その三角形は直角三角形であるというものです。図形の証明問題などに使われる場合があるので、覚えておきましょう。 三平方の定理の証明三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います
Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor
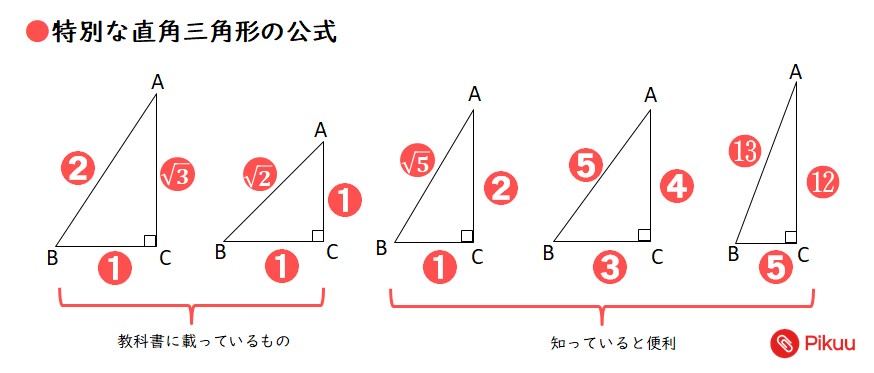
例 (1) 1 2 x 斜辺がxなので 1222=x2 x2 = 5 x > 0 より x= 5 (2) x 12 13 斜辺が13なので x2122 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方 三平方の定理の逆に関するまとめ 三平方の定理の逆はなぜ成り立つ? 間接証明法を使います 「 P P ならば Q Q 」の逆というのは「 Q Q ならば P P 」のこと。 つまり、 三平方の定理直角三角形であれば a 2 b 2 = c 2 a 2 b 2 = c 2 が成り立つ。 三平方
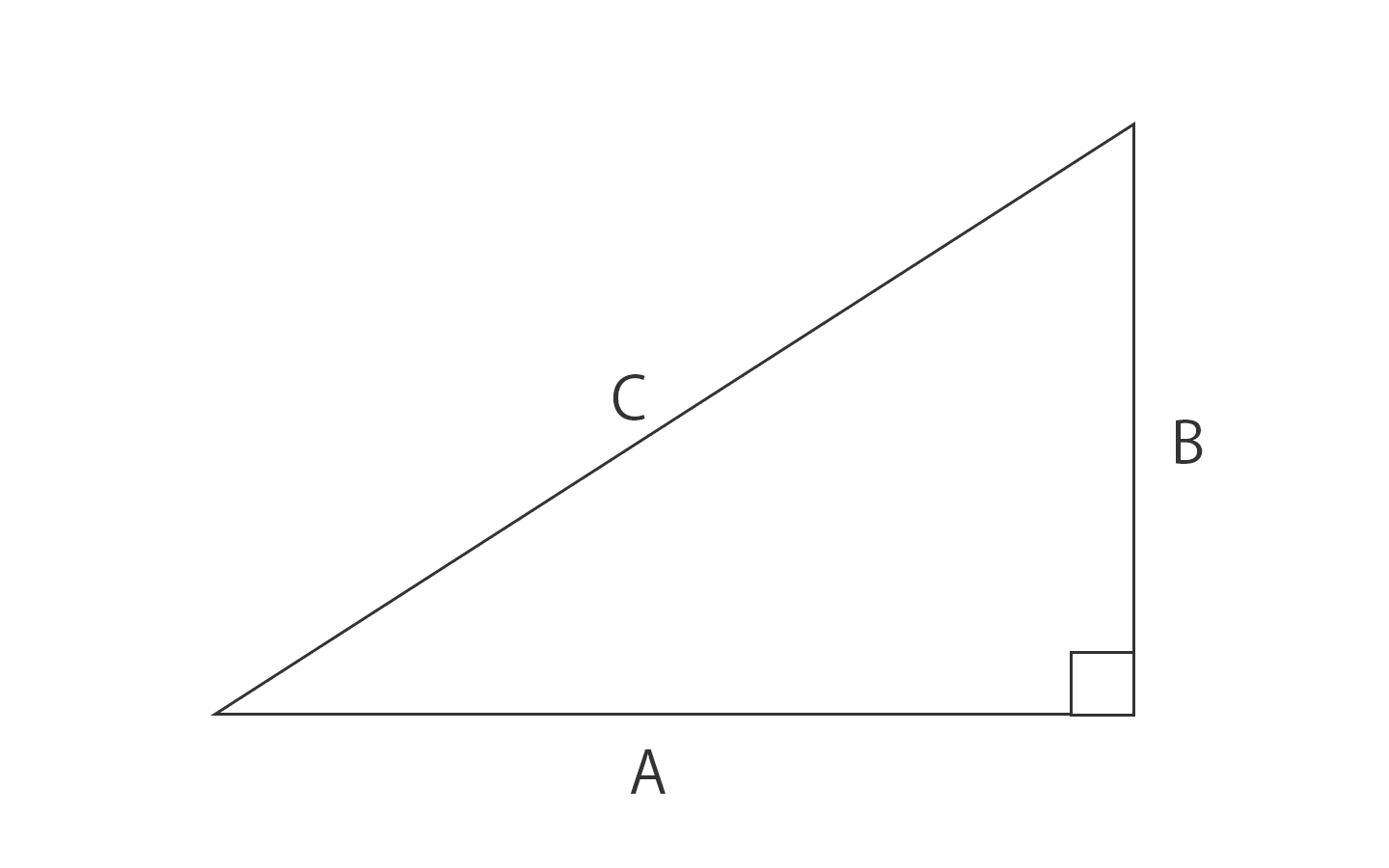
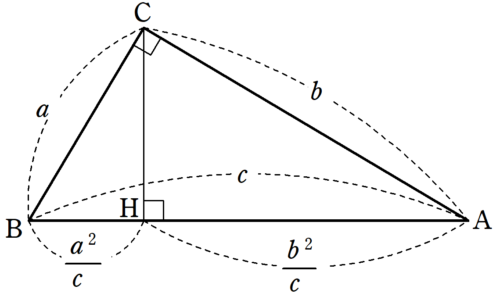
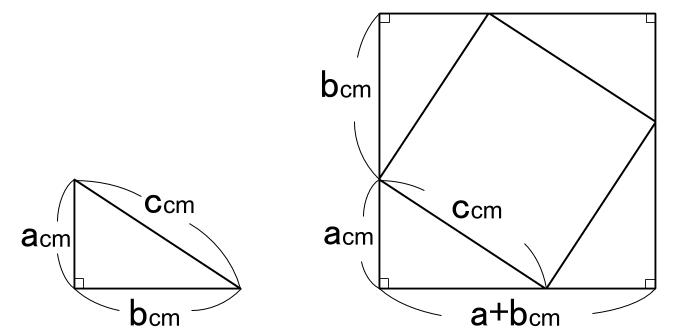
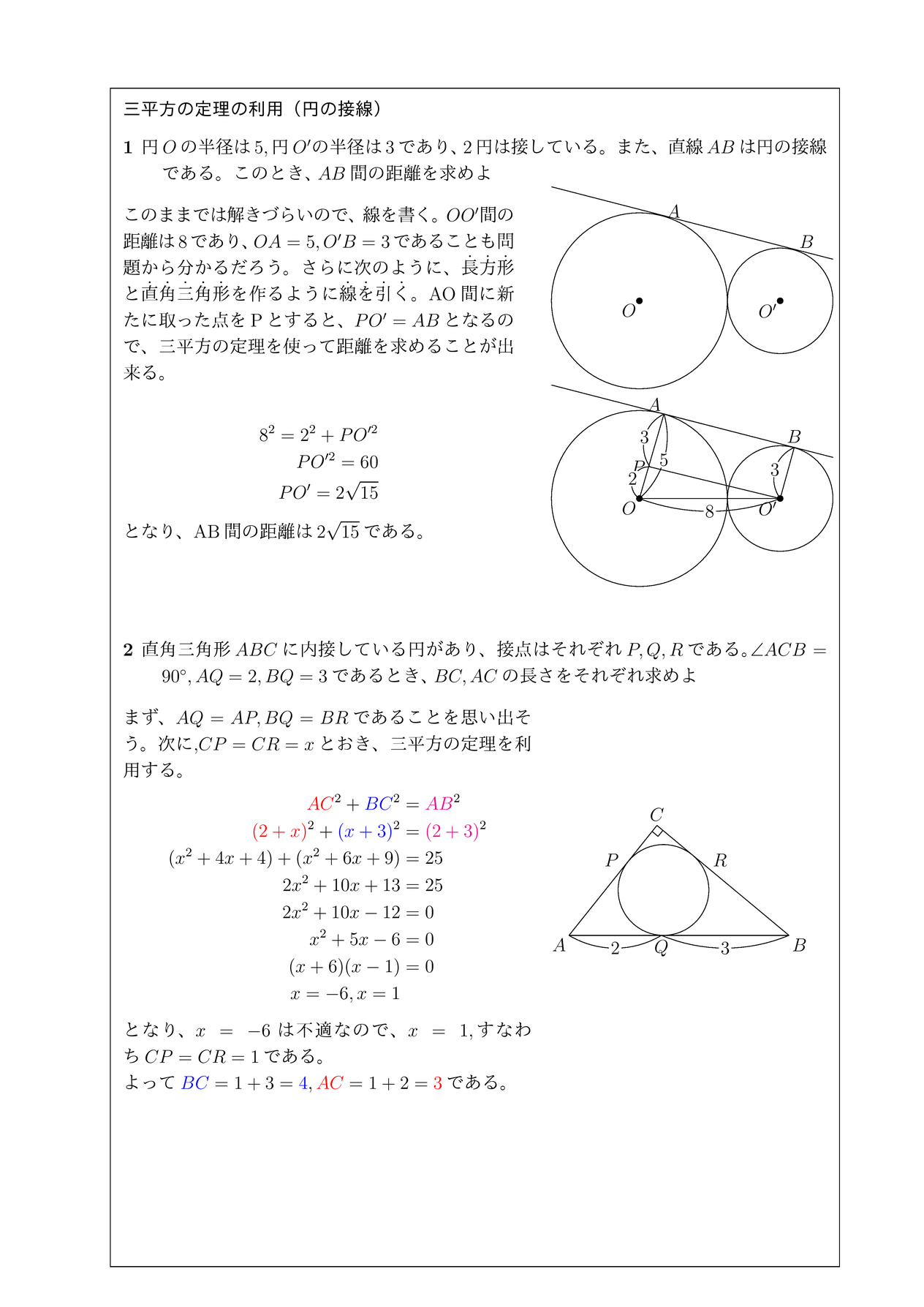
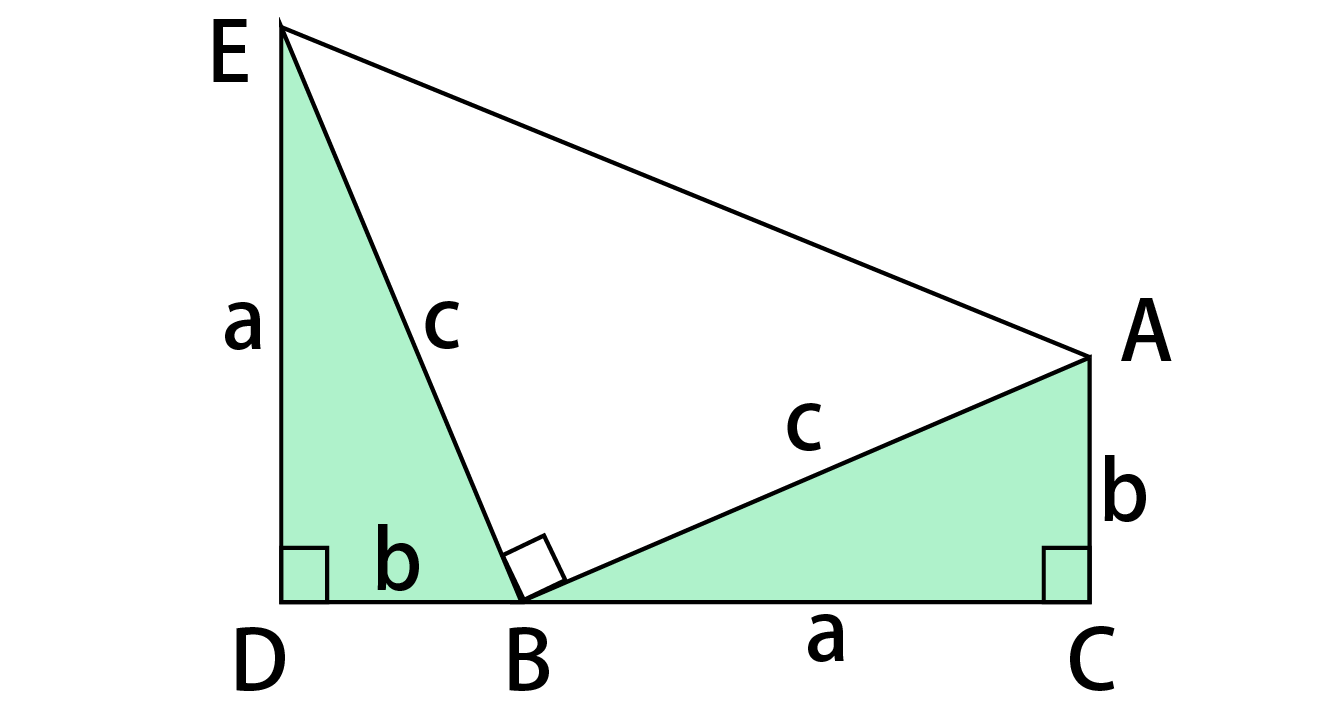
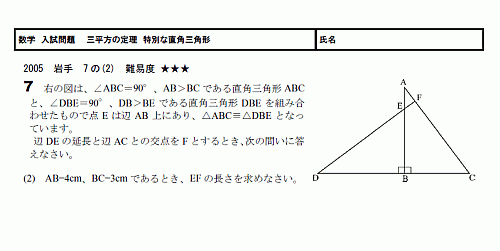
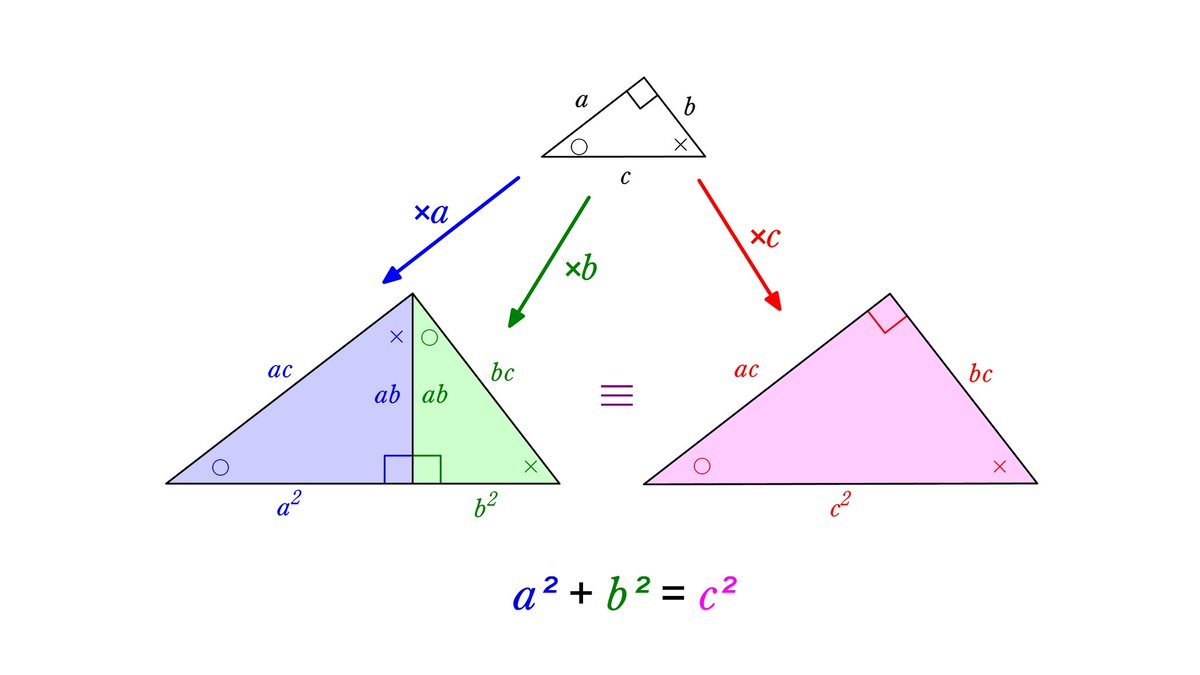
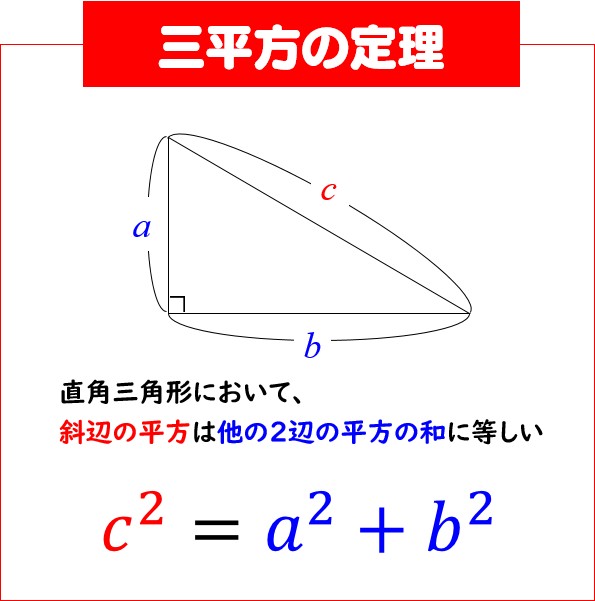
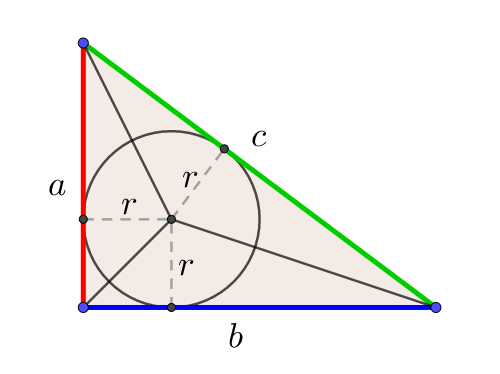
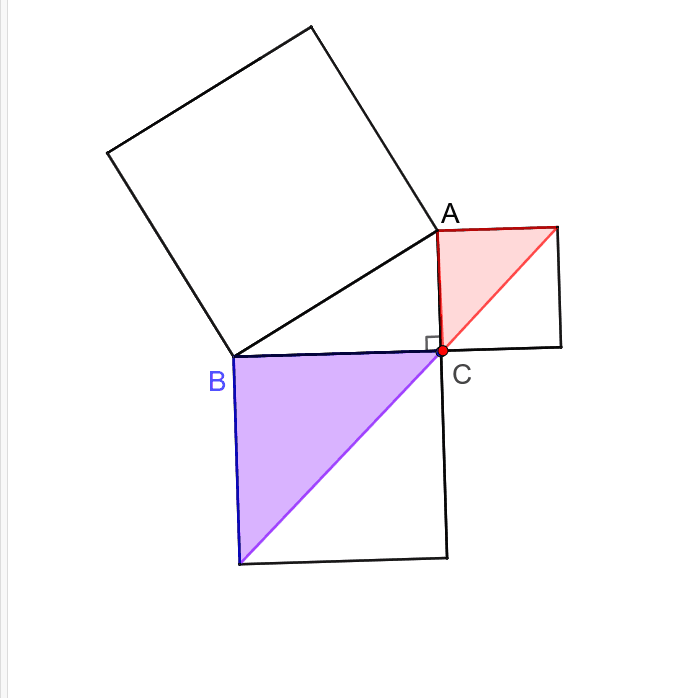
直角三角形ABD について三平方の定理を適用すると 22 (x1)2= (√13nnnnn)2 (x1)2=9 x1=3 (>0) x=2 例2 長方形の向かい合う辺の長さは等しいので,次の図で AH=DC になる. この AH の長さと AB の長さから三角形 ABH について三平方の定理を使うと辺 BH が求まり, HC 三平方の定理の証明5選直角三角形や正方形を重ねましょう 三平方の定理 (別名ピタゴラスの定理)とは、底辺が a a 、高さが b b 、斜辺が c c である直角三角形において、 a 2 b 2 = c 2 a 2 b 2 = c 2 が成り立つことでしたね。 この式を証明するポイントを三平方の定理 自動計算サイト 三平方の定理による辺の長さの計算です。 三平方の定理は、 直角三角形の三辺をa,b,cとする。 斜辺 (最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。 別名ピタゴラスの定理とも呼ばれます。
三角形 三平方の定理 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 三平方の定理 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
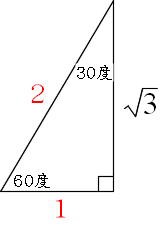
三平方の定理の証明|直感的に分かる図で解説します 管理人 5月 23, / 5月 27, 三平方の定理は直角三角形の辺の長さに関する定理ですが、今後、図形だけではなく関数などあらゆる分野でも利用することになる重要な定理です。 今回は三平方の定理 それで、三平方の定理を使えば、 2× 2 =√3×√3+ 1 × 1 になることは納得できます。 そのため、次の内容は正しいことになります。 3 つの辺が√3と 2 と 1 の三角形は直角三角形になり、内側の角度は 90 度、 60 度、 30 度になる このことは三平方の定理
Incoming Term: 三角形 三平方の定理, 三角形 三平方の定理 計算, 三角形 三平方の定理 証明,
コメント
コメントを投稿